How can you measure Uncertainty ?
How can you measure “uncertainty”? This was a question I have posed to my kids when they were learning probability. Understanding “uncertainty” is a good starting point to introduce a notion of entropy as well. I think the topic is interesting because understanding “uncertainty” using entropy is another way of learning about probability.
Let me start with a simple example of tossing a coin. If you have a fair coin, both events, HEADs and TAILs are equally likely to occur. You are uncertain about the outcome. For example, when you play a game of tossing a coin in a casino, you cannot really determine which side to bet in order to increase the odds of winning. But if you have information about a particular coin being not fair, such as 75% chance of getting a HEADs, you are somewhat certain about the outcome and can come up with a betting strategy. You can think of “all events occurring equally likely” as “minimum information”. Becoming more certain about the outcome can be interpreted as gaining more information. As you gain more information, you reduce uncertainty.
Then, how can you come up with a way to quantify “uncertainty”? Actually, this idea comes from Claude Shannon’s information theory, which I am going to explain the concept here for those who are not familiar with this subject.
I am going to define “entropy” as numbers that represent “uncertainty”. The value can range from 0 to x where x represents minimum information. As I have mentioned earlier, two (2) equally likely events (fair coin game) represent minimum information. How about throwing a fair dice? There are six (6) equally likely events which also represent minimum information. If I play both, I am more certain about playing the fair coin game than playing the fair dice game. In other words, as the number of events increases, the amount of uncertainty also increases. Definitely, more events increase uncertainty.
Now I have another question. Can I use the number of events to represent entropy? The answer is “maybe”, but there is a better way to represent entropy. Before answering this question, let’s talk about events in depth.
What is the number of all possible events when you toss a fair coin? There are HEADs and TAILs; so the number of events is 2. What is the number of possible events for the case of getting a ball out of the box with 4 different colored balls (4 equally likely events)? Obviously, it is 4. Let’s make it concrete. I am going to calculate the number of all possible events by dividing one (1) by the probability of the event. As you can see below, the number of “equally likely events” is the same as one (1) over the probability of getting that “equally likely events”.
# of all possible events = 1/p where p is the probability of the event.
“2” equally likely events case (fair coin: 50% or 1/2) : 1/p = 1 / (1/2) = “2”
“4” equally likely events case (25% or 1/4): 1/p = 1 / (1/4) = “4”
“6” equally likely events case (fair dice: ~0.1666% or 1/6): 1/p = 1 / (1/6) = “6”
Obviously, 50% chance of getting an event can be thought of getting two (2) out of four (4) chance (2/4) of getting an event. In this case, the number of all possible events is two (2).
# of all possible equally likely events case = 4
50% of 4 = 2/4 (= 1/2)
# of all possible events = 1/p = 1/(2/4) = 2
Now, how about 75% chance of getting an event? I can apply the same formula to get the number of all possible events.
# of all possible fair 4-events case = 4
75% of 4 = 3/4
# of all possible events = 1/(3/4) = 4/3 = ~1.3333
This is a little bit weird . You may say, what do you mean by “all possible events of 1.333~” ? Let me give you an example for clarity. If the probability of completing a task per year is 75%, how many years do I need? One (1) year or two (2) years? Probably, I can finish it within a year but there is a 25% chance I might not. So, I need a buffer. What if I consider that I can finish 75% of the task within a year? Then, I need a few more months to complete the task. In this case, I would need 4 more months (~0.3333 * 12). Similarly, if the probability of completing a task per year is 50%, I would probably need 2 years to complete the task. In this example, “all possible events” refers to the number of years I would probably need to complete the task.
Lastly, how about 100% chance of getting an event? Likewise, I can apply the same formula to get the number of all possible events. The answer is one (1) because I am 100% certain. If the probability of completing a task per year is 100%, I need exactly one (1) year to complete the task.
# of all possible fair 4-events case = 4
100% of 4 = 4/4
# of all possible events = 1/(4/4) = 1
Below is the summary of what I have discussed so far. My intention here is to show that one (1) over the probability of the event is the same as the number of possible events.

Let’s see whether I can use the number of events as a measure of uncertainty (entropy) or not. In order to express “uncertainty”, the number of events must be greater than one (1). If you only have one (1) event, you are always certain about getting that event. So, the entropy value should be zero (0) when I am 100% certain, but unfortunately, the number of event is one (1) as shown in Table 1. In addition, entropy quickly becomes large when the number of events increases. For example, the entropy value for 256 events is 256.
In Table 1, I have deliberately selected the number of “equally likely events” that correspond to numbers to the power of two (2) except cases highlighted in yellow. Let’s pay attention to the exponent. It seems to me that the number of “four (4) equally likely events” (25%) is equivalent to the square of the number of “two (2) equally likely events” (50%). What if I use eight (8) equally likely events or sixteen (16) equally likely events? The number of “equally likely events” for these two cases also correspond to the cube and quad of the number of “two (2) equally likely events”.
I think the exponent is a good candidate to represent entropy. As the number of events increases or equivalently as the probability of events decreases (1/2, 1/4, 1/8, 1/16, …), the entropy value (or uncertainty) increases (1, 2, 3, 4). In addition, entropy for the single event case can now be expressed as zero (0). Conveniently, this is equivalent to using “events on a log scale” to determine “entropy” values.
Then, you may ask, why log base 2? I think it has to do with Claude Shannon’s information theory where the binary digit (bit) is considered as the unit of communication. In the case of “fair coin”, you can transmit either HEADs or TAILs in one (1) bit. But if the coin is unfair (75% HEADs and 25% TAILs), you can transmit information in ~0.42 bit. As the certainty of getting a HEADs increases from 50% to 75%, the uncertainty decreases. By how much? Let me give you some examples to make this concept more concrete.
Let’s assume that I have an unfair coin, and the probability of getting a HEADs is 75% whereas the probability of getting TAILs is 25%. I would like to know the entropy of this unfair coin.
But, let me start with a fair coin before addressing this unfair coin case.
Entropy(HEADs=1/2) = Entropy(1/2) = log2 (1/0.5) = log2 (2) = 1
Entropy(TAILs=1/2) = Entropy(1/2) = log2 (1/0.5) = log2 (2) = 1
The resulting value, one (1) represents minimum information in the case of tossing a fair coin. The event, HEADs contributes one half of this entropy, which is 0.5. Likewise, the event, TAILs also contributes the same amount.
Entropy(50% HEADs and 50% TAILs) = 0.5*Entropy (1/2) + 0.5*Entropy (1/2)
= (1/2) * log2 (2) + (1/2) * log2 (2)
= (0.5)*(1) + (0.5)*(1)
= 1
As you can see, the minimum information for the “two (2) equally likely event” case is one (1). If you apply the same formula for four (4), six (6) and eight (8) equally likely event cases, you will get 2, ~2.58 and 3 as shown in the “Log scale” column of Table 1.
Now I am going to calculate entropy values of 75% HEADs and 25% TAILs. Since I am more certain about getting a HEADs, I expect to see a lower entropy value in this case.
Entropy(HEADs=3/4) = Entropy(3/4) = log2 (1/0.75) = log2 (4/3) = ~0.42
Entropy(TAILs=1/4) = Entropy(1/4) = log2 (1/0.25) = log2 (4) = 2
Then, the entropy value for the unfair coin case is calculated as shown below.
Entropy(75% HEADs and 25% TAILs) = 0.75*Entropy (3/4) + 0.25*Entropy (1/4)
= (3/4) * log2 (4/3) + (1/4) * log2 (4)
= (0.75)*(~0.42) + (0.25)*(2) = ~0.31 + 0.5
= ~0.81
As you can see, the uncertainty (entropy) decreases from 1 to ~0.81.
How about calculating entropy values of “99.99999% HEADs and 0.00001% TAILs” ? This should be close to zero (0). Let’s find out.
Entropy(HEADs=99.99999%) = log2 (1/0.9999999)
Entropy(TAILs=0.00001%) = log2 (1/0.0000001)
Entropy(HEADs=99.99999%) and Entropy(TAILs=0.00001%)
= 0.9999999*log2 (1/0.9999999) + 0.0000001*log2 (1/0.0000001)
= ~0.0000025
As you can see, as the probability reaches one (1) or 100% (certainty), the entropy approaches zero (0).
Finally, I can answer this question: how can you come up with a way to quantify “uncertainty”? Let’s me formalize the formula using a fair dice example:



I can also use the summation notation to simplify the formula:

Finally, I can generalize it:
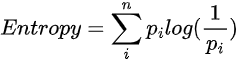
You can also express it as below:

I hope the concept of “entropy” and how to drive its formula makes complete sense.
Comments
Post a Comment